在浏览论坛或评论区的时候，你可能偶尔会遇到一种奇妙的现象：一张图片，在点击放大查看时，呈现出来的内容竟然和最初看到的缩略图完全不同！这个现象让我非常好奇，经过探究我理解了其背后的原理，并且编写了一个简易工具来方便地创建这种图片。

2025/04/05 更新：新版本支持彩色图片，并且优化了原理解释部分。

1 效果展示

下面是一张我制作的可变图片，尝试点击进入大图页面，看看它是不是会变化吧！在博客左上角切换日间/夜间模式同样也可以让图片变化。

由于本博客进入大图页面/夜间模式后，背景并非纯黑 #000000，而是灰色 #242424，因此会看到一些重影，属于正常情况。

1.1 灰度模式

灰度模式的效果可以达到完美，只要满足切换条件，即使表里图片完全不一样，也能够非常完美得切换，但唯一的缺点就是不能保留图片的色彩。

这个模式是我最先研究出来的，在 v1.0.0 中就支持灰度模式了，不过当时使用的是棋盘法。在 v1.2.0 中引入了新的直接混合法，生成效果更加好，兼容性更强。

1.2 彩色模式

在 v1.2.0 中引入的直接混合法可以生成彩色的可变图片了！可以看到下图的效果还是非常棒的，终于是彩色的了。

可惜的是，彩色图有一点限制条件，只有表里图片相近的情况下才能有比较好的混合结果。

如果表里图片是完全不一样的彩色图片，那么会有严重的混色情况，虽说也能切换，但是颜色就非常混乱了。退而求其次得话，可以仅开启表/里其中一个图片的彩色模式，这样能够一定程度缓解问题。

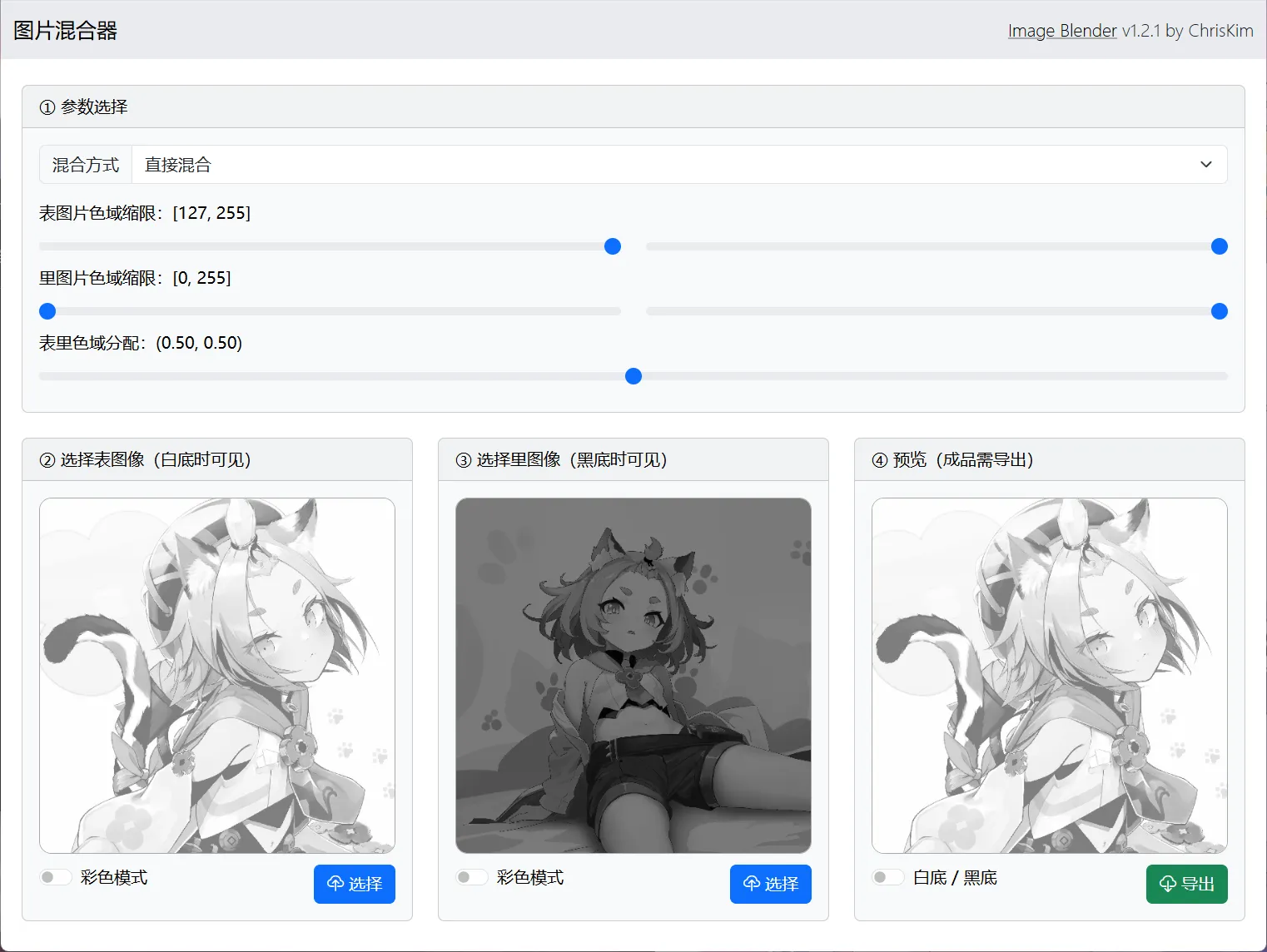
2 小工具

我编写了一个小工具，大家只需要准备两个图像，分别作为表层和里层就可以生成可变图像了。该工具的计算全部由本地浏览器完成，选择的图片不会发送到我的服务器，因此可以放心使用。

由于图片是本地处理的，因此不要上传过大的图片，以免把浏览器卡死。电脑端测试时 6400*6400 的图片可以正常处理，如果出现卡死的情况，可以尝试降低图片分辨率。

工具链接为：https://www.chriskim.cn/image-blender

工具代码已经开源在 GitHub，如果觉得写的不错可以给我点星哦~

3 原理说明

如果你觉得只会用工具制作还不够，想要了解其中原理，那么可以接着往下看。

3.1 透明叠加规则

首先，我们要了解含透明通道的图片叠加时的融合规则。

若有图片 $I^{\text{A}}$ 与 $I^{\text{B}}$，图片 $I^{\text{A}}$ 叠加在图片 $I^{\text{B}}$ 的上面，叠加后形成的图片记为 $I^{\text{C}}$，图片每个像素分为颜色通道和透明度通道 $I_{i,j}=(C_{i,j},\alpha_{i,j})$，那么混合后的图片颜色 $C_{i,j}$ 和透明度 $\alpha_{i,j}$ 按以下公式计算：

$$
\begin{align}
C^{\text{C}}_{i,j}=\alpha^{\text{A}}_{i,j}\cdot C^{\text{A}}_{i,j}+\alpha^{\text{B}}_{i,j}\cdot C^{\text{B}}_{i,j}\\
\alpha^{\text{C}}_{i,j}=\alpha^{\text{A}}_{i,j}+(1-\alpha^{\text{A}}_{i,j})\alpha^{\text{B}}_{i,j}
\end{align}
$$

简单来说，结果图像的颜色是基于两个图像的颜色和它们各自的透明度加权混合得到的，而最终图像的透明度则反映了两者透明度的组合效果。

3.2 问题描述

要实现可变图像，该问题用数学表达如下。

表图片 $I^{\text{outer}}$ 与里图片 $I^{\text{inner}}$ 尺寸相同，高宽分别为 $h,w$，通过一些方法将两图片进行混合，得到结果图片 $I^{\text{result}}$。同时，结果图片满足以下条件 $I^{\text{result}}$：

1. 在白色背景下，结果图片与表图片相近，即 $I^{\text{result}}+I^{\text{white}}\approx I^{\text{outer}}$.
2. 在黑色背景下，结果图片与里图片相近，即 $I^{\text{result}}+I^{\text{black}}\approx I^{\text{inner}}$.

3.3 直接混合法

直接混合法中，表里图片均占用所有像素，但是表里图片分别占用每个像素通道值的一半。将图片记为颜色通道+透明度通道 $I=(C,\alpha)$，那么背景与图片的混合公式为：

$$
C=\alpha\cdot C^{\text{image}}+(1-\alpha)C^{\text{background}}
$$

那么可列出以下方程组：

$$
\begin{cases}
C^{\text{outer}}=\alpha\cdot C^{\text{result}}+(1-\alpha)C^{\text{white}}=\alpha\cdot C^{\text{result}}+1-\alpha\\
C^{\text{inner}}=\alpha\cdot C^{\text{result}}+(1-\alpha)C^{\text{black}}=\alpha\cdot C^{\text{result}}
\\ \end{cases}
$$

解得：

$$
\begin{cases}
\displaystyle{\alpha=1-C^{\text{outer}}+C^{\text{inner}}}\\ \displaystyle{C^{\text{result}}=\frac{C^{\text{inner}}}{1-C^{\text{outer}}+C^{\text{inner}}}}
\end{cases}
$$

根据以上解混合图片即可。如果 $C$ 通道为灰度图，则按照该公式混合，如果 $C$ 通道是三维的向量，那么代表向量每个分量对应做计算，即 RGB 通道分别计算。

3.4 棋盘混合法

棋盘混合法中，表里图片分别占用一半的像素。结果图片为一个马赛克网格，每个像素交错为白色与黑色：

$$
C^{\text{result}}_{i,j}=
\begin{cases}
(0,0,0) & \text{if } (i+j)\bmod 2=0\\
(1,1,1) & \text{if } (i+j)\bmod 2=1
\end{cases}
$$

用图片来可视化表示，那么颜色如下：

黑色像素负责表层图片的显示，白色像素负责里层图片的显示。既然图片 C 的颜色已经固定了，那就说明它显示的图案仅取决于透明度：

$$
\alpha_{i,j}^{\text{result}}=
\begin{cases}
1-\alpha_{i,j}^{\text{outer}} & \text{if } (i+j)\bmod 2=0\
\alpha_{i,j}^{\text{inner}} & \text{if } (i+j)\bmod 2=1\
\end{cases}
$$

根据以上解混合图片即可。

此种方法，当使用白色背景时，白色像素被屏蔽，白色背景与黑色像素透明度混合显示表层图片；当使用黑色背景时，黑色像素被屏蔽，黑色背景与白色像素透明度混合显示里层图片。